変数活性度と変数割当て量の相関
以下は変数活性度の分散(青色の線)と変数割当量のEMA(緑色の線)の時間変化である。
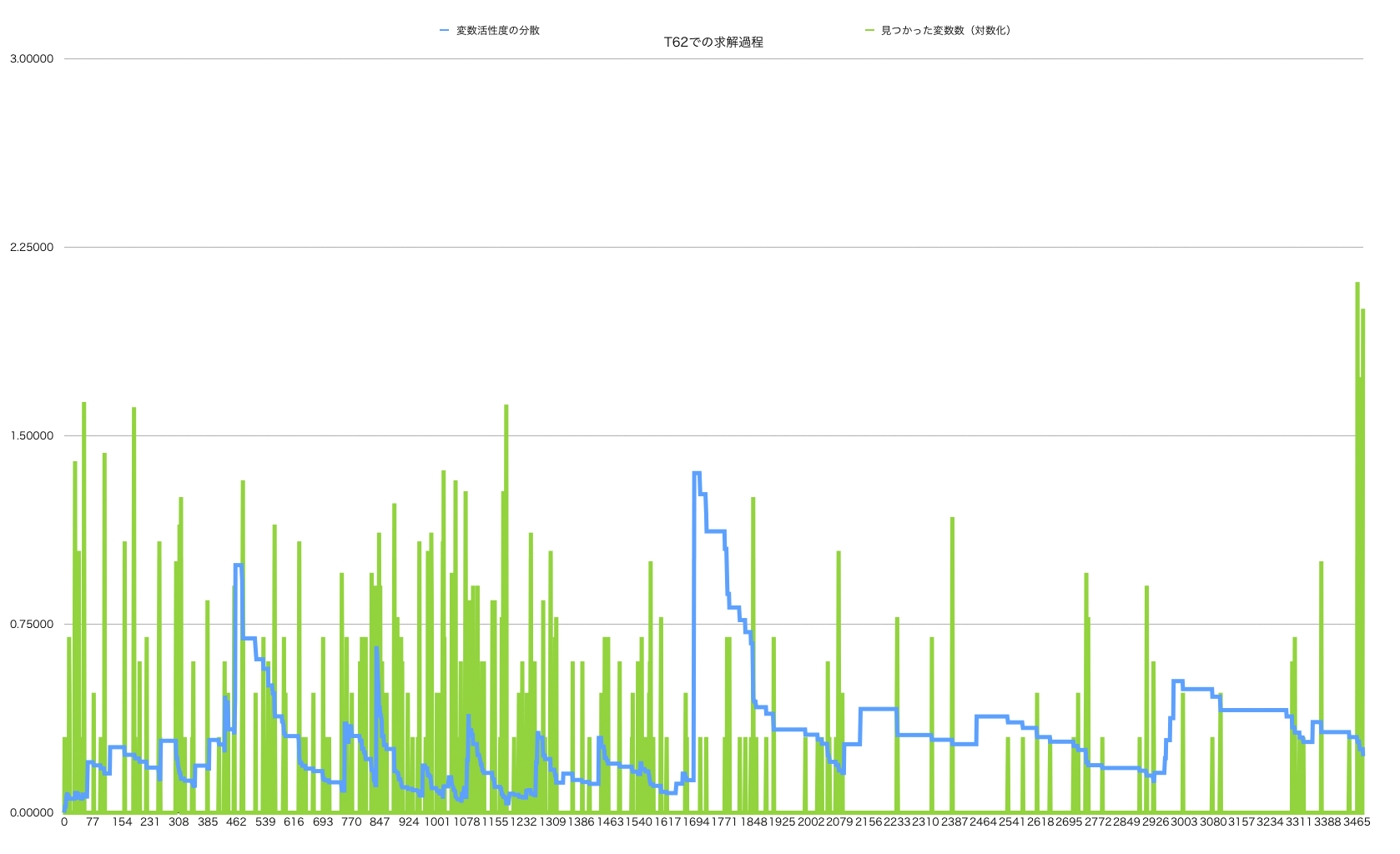
どうもこの両者には負の相関があるらしい。変数割当てが減ると分散は高くなる。 これは、
- リスタートにより活性度が高い変数群の割当てを優先する。 他の変数の割当てはなくなり、全体としての割当量は減少する。
- リスタート後もその矛盾する変数に関連する変数のみ活性度が繰り返し増加する。 従って活性度の分散は大きくなる。
ということで説明できるだろう。
難しい山を乗り越えたからこそ(変数割当てに関する)進捗があるらしい。 逆に、割当量が小さくなりながら(困難な矛盾が解決して)新しい変数が見つかる。 とは言え、決して小ささを維持しようとしているわけではない。 小さくなった後では大したことはできないと思う。
逆に言うと、落ちるためにまず上がらなければならないのかもしれないが、これは当然、予測不能問題:
- 今、超えないといけないから山を登るべきなのか、
- 高すぎる=資源を使いすぎたから降りるべきなのか。
しかし、それでもstagnationは
- threshold
- step
- 山登り量
のどれかの増加の契機となるはずではなかろうか。
2019-07-13
割当て率と平均LBDをガイドにした場合ほど性能がよくない。目的関数にするには、ずれているのかも。確かに割当てを改善しなければ解には到達できないだろう。しかし枝刈りの尺度としては優秀なはずなのだが。
分散は目的ではなく求解過程の(遷移)状態を表現しているのかも。